Vector Cross Product

Cross Product

Definition

The cross product of two vectors is defined as follows

(1)

\begin{align} \vec{u}\times\vec{v}=(|\vec{u}||\vec{v}|\sin \theta)\hat{n} \end{align}

where the vector $\hat{n}$ is a vector of unit length that is perpendicular to both the vector $\vec{u}$ and $\vec{v}$. The direction of the vector is determined by the right-hand rule. Point your fingers in the direction of $\vec{u}$ and curl them in the direction of $\vec{v}$ and your thumb will point in the direction of $\hat{n}$

Because of the right-hand rule, if you switch the order of the vectors, $\hat{n}$ switches to the opposite direction. Therefore, $\vec{u} \times \vec{v}=-(\vec{u} \times \vec{v})$

Since $\hat{n}$ is a unit vector, $\vec{u} \times \vec{v}$ is written as the product of its magnitude and direction. Where the direction of $\vec{u} \times \vec{v}$ is $\hat{n}$ and $|\vec{u} \times \vec{v}|=|\vec{u}||\vec{v}|\sin \theta$

Example
Find the magnitude of the cross product of $\vec{u}=15@45^\circ$ and $\vec{v}=4@100^\circ$

Solution

$|\vec{u}|=15$
$|\vec{v}|=4$
The angle between the two vectors is $\theta= 100 - 45 = 55 ^\circ$
So $|\vec{u} \times \vec{v}| = (15)(4)\sin 55 ^\circ \approx 60(0.829)=49.149$

Notice that if $\vec{u}$ and $\vec{v}$ are parallel then,

(2)

\begin{align} \vec{u}\times\vec{v}=(|u||v|\sin 0^\circ)\hat{n}=0\hat{n}=\vec{0} \end{align}

or

(3)

\begin{align} \vec{u}\times\vec{v}=(|u||v|\sin 180^\circ)\hat{n}=0\hat{n}=\vec{0} \end{align}

Calculating the Cross Product

For the purposes of calculation, this definition is not usually useful. It does not explicitly tell us how to find the vector $\hat{n}$. Instead, if we are given two vectors in component form

(4)

\begin{eqnarray} \vec{u}&=&<u_x,u_y,u_z>\\ \vec{v}&=&<v_x,v_y,v_z>\\ \end{eqnarray}

then

(5)

\begin{align} \vec{u}\times\vec{v}= \left | \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ u_x& u_y & u_z\\ v_x & v_y & v_z \\ \end{array} \right | =(u_yv_z-v_yu_z)\hat{i}-(u_xv_z-v_xu_z)\hat{j}+(u_xv_y-v_xu_y)\hat{k} \end{align}

Unlike other operations the cross product is not commutative. That is to say $\vec{u}\times\vec{v}\neq\vec{v}\times \vec{u}$.

(6)

\begin{align} \vec{v}\times\vec{u}= \left | \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ v_x& v_y & v_z\\ u_x & u_y & u_z \\ \end{array} \right | =(v_yu_z-u_yv_z)\hat{i}-(v_xu_z-u_xv_z)\hat{j}+(v_xu_y-u_xv_y)\hat{k}=-(\vec{u}\times\vec{v}) \end{align}

Finding the Equation of a Plane

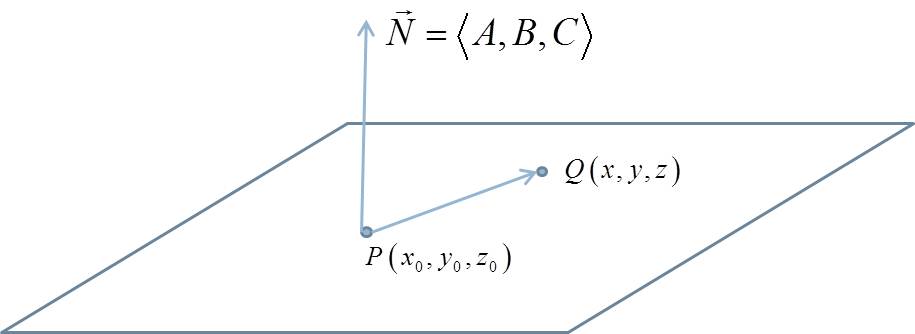
We describe a plane by a point on the plane, $P(x_0,y_0,z_0)$, and a vector perpendicular to the plane called a normal vector, $\vec{N}=<A,B,C>$. Looking at the image below, notice that any vector that we create in the plane will be perpendicular to $\vec{N}$. So the vector $\vec{PQ}=<x-x_0,y-y_0,z-z_0>$ is perpendicular to $\vec{N}=<A,B,C>$. We know, that for perpendicular vectors, the dot product is zero. Therefore we have,

(7)

\begin{eqnarray} \vec{N} \cdot \vec{PQ} = 0\\ <A,B,C>\cdot <x-x_0,y-y_0,z-z_0>=0\\ A(x-x_0)+B(y-y_0)+C(z-z_0)=0 \end{eqnarray}

The standard equation of a plane containing a point $P(x_0,y_0,z_0)$ that has a normal of $\vec{N}=<A,B,C>$ is therefore,

(8)

\begin{equation} A(x-x_0)+B(y-y_0)+C(z-z_0)=0 \end{equation}

In two dimensions, we know that two unique points will define a line. In three dimensions, the analog is that three non-collinear points, not on a common line, will define a plane. Given those three points, we can construct two nonparallel vectors that lie in the plane. If we take the cross product of those two vectors, we will get a vector perpendicular to the plane. We can use that cross product as the $\vec{N}$ for our plane.

Example
Find the equation of the plane containing the points $P(5,1,1)$ , $Q(0,2,2)$ , and $R(6,2,0)$

Solution

First we create our two vectors in the plane
$\vec{u}=\vec{PQ}=<0-5,2-1,2-1>=<-5,1,1>$
$\vec{v}=\vec{PR}=<6-5,2-1,0-1>=<1,1,-1>$
Now we find our $\vec{N}$ for the plane
$\vec{N}=\vec{u}\times\vec{v}= \left |\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k}\\-5 & 1 & 1\\1 & 1 & -1\\\end{array}\right |=(-1-1)\hat{i}-(5-1)\hat{j}+(-5-1)\hat{k}=-2\hat{i}-4\hat{j}-6\hat{k}$
Now using our $\vec{N}$ along with a point, say $P$ we can write our equation for the plane.
$-2(x-5)-4(y-1)-6(z-1)=0$
$-2x+10-4y+4-6z+6=0$
$-2x-4y-6z=-20$
$x+2y+3z=10$

Finding the Area of a Parallelogram

We know from geometry that the area of a parallelogram is given by $A=bh$. In the image below we see that the area of the parallelogram would be,

(9)

\begin{eqnarray} A=|\vec{u}|h\\ \end{eqnarray}

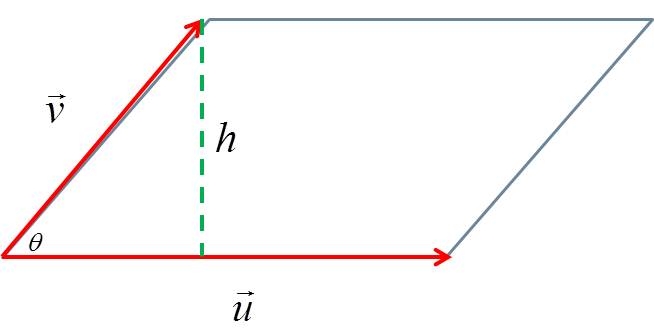
But from right triangle trigonometry we have that,

(10)

\begin{eqnarray} \sin \theta = \frac{h}{|\vec{v}|}\\ h=|\vec{v}|\sin \theta \end{eqnarray}

Combining the facts from 9 and 10, we have that

(11)

\begin{eqnarray} A=|\vec{u}|h\\ A=|\vec{u}||\vec{v}|\sin \theta\\ A=|\vec{u} \times \vec{v}| \end{eqnarray}

So the area of the parallelogram whose nonparallel sides are the vectors $\vec{u}$ and $\vec{v}$ can be calculated by the formula

(12)

\begin{align} \mbox{Area}=|\vec{u} \times \vec{v}| \end{align}

Example
Find the area of the parallelogram with vertices $P(1,1)$ , $Q(5,1)$ , $R(3,3)$ and $S(7,3)$

Solution

First we create our two vectors representing non-parallel sides of the parallelogram
$\vec{u}=\vec{PQ}=<5-1,1-1>=<4,0>$
$\vec{v}=\vec{PR}=<3-1,3-1>=<2,2>$
Now we find our $\vec{PQ} \times \vec{PR}$
$\vec{PQ}\times\vec{PR}= \left |\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k}\\4 & 0 & 0\\2 & 2 & 0\\\end{array}\right |=(0-0)\hat{i}-(0-0)\hat{j}+(8-0)\hat{k}=-0\hat{i}+0\hat{j}+8\hat{k}$
So, $A=|\vec{PQ} \times \vec{PR}|=\sqrt{0+0+64}=8$

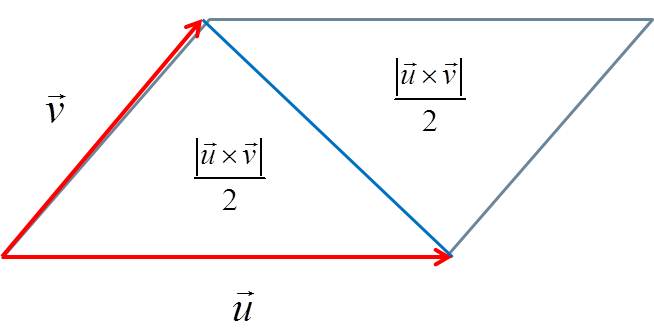
Finding the Area of a Triangle

Since a triangle can be thought of as half of a parallelogram, the area of the triangle with two sides defined by $\vec{u}$ and $\vec{v}$ can be calculated by the formula

(13)

\begin{align} \mbox{Area}=\frac{1}{2}|\vec{u} \times \vec{v}| \end{align}

Example
Find the area of the triangle with vertices $P(1,1,1)$ , $Q(2,1,0)$ and $R(-1,4,2)$

Solution

First we create our two vectors representing two sides of the triangle
$\vec{u}=\vec{PQ}=<2-1,1-1,0-1>=<1,0,-1>$
$\vec{v}=\vec{PR}=<-1-1,4-1,2-1>=<-2,3,1>$
Now we find our $\vec{PQ} \times \vec{PR}$
$\vec{PQ}\times\vec{PR}= \left |\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k}\\1 & 0 & -1\\2 & 3 & 1\\\end{array}\right |=(0+3)\hat{i}-(1-2)\hat{j}+(3-0)\hat{k}=3\hat{i}+1\hat{j}+3\hat{k}$
So, $A=\frac{|\vec{PQ} \times \vec{PR}|}{2}=\frac{\sqrt{9+1+9}}{2}=\frac{\sqrt{19}}{2} \approx 2.2$

Exercises

1. Find the magnitude of the cross product of $11@15^\circ$ and $99@-15^\circ$
2. Find the cross product of $\vec{u}=<1,-1,2>$ and $\vec{v}=<0,2,-1>$.
3. The points (1,1,3), (2, -3, 3), and (-1, 0, 4) determine a plane. Find the equation of the plane in both standard and dot product form.
4. Use cross product to show that $\vec{u}=<1,4,-5>$ and $\vec{v}=<-3,-12,15>$ are parallel.
5. Find the area of the parallelogram with vertices (0,0) , (3,7) , (2,5) and (5,12)
6. Find the area of the parallelogram with vertices (0,0,0) , (3,2,4) , (5,1,4) and (2,-1,0)
7. Explain, in terms of the definition, why $\vec{u} \times \vec{v} = -(\vec{v} \times \vec{u})$
8. Find the area of the triangle with vertices (1,2,-1) , (4,1,0) and (3,8,1)
9. Find the area of the triangle with vertices (1,-1,2) , (2,0,-1) and (0,2,1)
10. Find a vector perpendicular to the plane $5x-3y+6z=8$
11. If the vectors $\vec{u}$ and $\vec{v}$ are 3D vectors parallel to the xy-plane, what do we know about their cross-product?