Dot Product
The dot product of two vectors results in a scalar. The dot product can be calculated in either of the following ways.
(1)
The dot product in some way is the measure of how much the two vectors agree in their directions. Either $\vec{u}$ in the direction of $\vec{v}$ or $\vec{v}$ in the direction of $\vec{u}$. In the case where one of the vectors, say $\vec{u}$, is a unit vector this sense is exact.
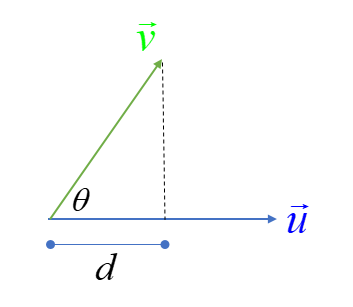
From trigonometry, we see that $d=|\vec{v}|\cos \theta$, but since we are assuming $\vec{u}$ is a unit vector, we have $\vec{u} \cdot \vec{v} = |\vec{u}||\vec{v}|\cos \theta=|\vec{v}|\cos \theta = d$
Exercise
Find the dot product of $\vec{u}=\left < 1,4,-2 \right >$ and $\vec{v}=\left <-7,0,8 \right >$
Exercise
Find the dot product of $\vec{u}=20@80^\circ$ and $\vec{v}=12@10^\circ$
The Angle Between Two Vectors
The angle $0^\circ \leq \theta \leq 180^\circ$ made by the vectors $\vec{u}$ and $\vec{v}$ when they are placed with their initial points coinciding is given by
(3)Therefore,
(4)Recall that arccosine has a range from $0^\circ$ to $180^\circ$, which is exactly the range of values that the angle between two vectors can take on. Therefore, there is no need for any quadrant checks with this calculation.
Exercise
Find the angle between $\vec{u}=\left < -2,6,10 \right >$ and $\vec{v}=\left <2,4,0 \right >$
Perpendicular Vectors
Two vectors are perpendicular if their dot product equals zero. This can easily be seen from the above Eq.(2). When two vectors are perpendicular, the anlge between them is $90^\circ$. We know that $\cos 90^\circ=0$. Therefore, the dot product will be,
(5)We can take this analysis a step further. Also recall that $-1 \leq \cos \theta \leq 1$. Therefore, the dot product will be largest and equal to $|\vec{u}||\vec{v}|$ when $\cos \theta=1$ or when the angle between the two vectors is $0^\circ$. In other words, when the vectors are pointing in the same direction.Likewise, the dot product will be smallest and equal to $-|\vec{u}||\vec{v}|$ when $\cos \theta=-1$ or when the angle between the two vectors is $180^\circ$. In other words, when the vectors are pointing in opposite directions.
Exercise
Show that $\vec{u}=\left < -3,5,-1 \right >$ and $\vec{v}=\left <1,2,7 \right >$ are perpendicular
Exercise
Determine the value of $a$ such that $\vec{u}=\left < 4,5,6 \right >$ and $\vec{v}=\left <2,a,-3 \right >$ are perpendicular
Exercises
- Find the dot product of the vectors $<6, 8, –5>$ and $<–7, 3, 4>$.
- Find the dot product of the vectors 27 @ 35º and 19 @ 46º.
- Find the angle between the vectors $4\hat{x}+9\hat{y}$ and $-3\hat{x}+5\hat{y}$.
- Find the angle between the vectors $<6, 8, –5>$ and $<–7, 3, 4>$.
- Are the vectors $4\hat{x}+9\hat{y}$ and $-7\hat{x}+3\hat{y}$ perpendicular? Why or why not?
- Are the vectors $<8,6,-2>$ and $<7,5,13>$ perpendicular? Why or why not?
- Are the vectors $<8,6,-2>$ and $<-4,5,-1>$ perpendicular? Why or why not?